Цифровая обработка сигналов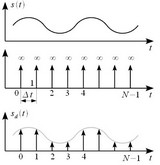
Дискретизация сигнала Сущность цифровой обработки состоит в том, что физический сигнал (напряжение, ток и т. д.) преобразуется в последовательность чисел, которая затем подвергается математическим преобразованиям в вычислительном устройстве. Трансформированный цифровой сигнал (последовательность чисел) при необходимости может быть преобразован обратно в напряжение или ток. Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты времени, называют аналоговыми (analog). Последовательность чисел, представляющая сигнал при цифровой обработке, является дискретным рядом (discrete series) и не может полностью соответствовать аналоговому сигналу. Числа, составляющие последовательность, являются значениями сигнала в отдельные (дискретные) моменты времени и называются отсчетами сигнала (samples). Как правило, отсчеты берутся через равные промежутки времени T, называемые периодом дискретизации (или интервалом, шагом дискретизации — sample time). Величина, обратная периоду дискретизации, называется частотой дискретизации (sampling frequency): Fd = 1/Т. 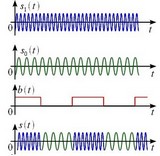
FSK сигнал Ясно, что в общем случае представление сигнала набором дискретных отсчетов приводит к потере информации, так как мы ничего не знаем о поведении сигнала в промежутках между отсчетами. Однако, как показывает Теорема Котелыгакова, существует класс аналоговых сигналов, для которых такой потери информации не происходит и которые могут быть точно восстановлены по значениям своих дискретных отсчетов. Процесс преобразования аналогового сигнала в последовательность от счетов называется дискретизацией (sampling), а результат такого преобразования — дискретным сигналом. При обработке сигнала в вычислительных устройствах его отсчеты представляются в виде двоичных чисел, имеющих ограниченное число разрядов. Вследствие этого отсчеты могут принимать лишь конечное множество значений и, следовательно, при представлении сигнала неизбежно происходит его округление. Процесс преобразования отсчетов сигнала в числа называется квантованием по уровню (quantization), а возникающие при этом ошибки округления — ошибками (или шумами) квантования (quantization error, quantization noise). Сигнал, дискретный во времени, но не квантованный но уровню, называется дискретным (discrete-time) сигналом. Сигнал, дискретный во времени и квантованный по уровню, называют цифровым (digital) сигналом. Сигналы, квантованные по уровню, но непрерывные во времени, на практике встречаются редко. Перечень докладов секции Цифровая обработка сигналов:
Внимание,по всем вопросам участия в семинаре и тематике его проведения Вы можете обратиться непосредственно к руководителю семинара — к.ф.-м.н., Сергею Викторовичу Кривальцевичу по электронной почте: radioseminar@радиосеминар.рф. |
Секции семинара:

|
| 2010–2024 Сергей Кривальцевич |